Antenna arrays
An antenna array is a group of multiple radiating elements whose signals are combined in such a way the overall radiation pattern is reinforced in certain desired direction and suppressed in other undesired directions. The combined radiation pattern of the system can be controlled by means of five parameters:
- The geometrical distribution of the unitary elements (i.e., linear, circular, rectangular, spherical, etc.).
- The relative displacement between the elements.
- The excitation amplitude of the individual elements.
- The excitation phase of the individual elements.
- The relative pattern of the individual elements.
Two-element array
Let us consider the simple case of an antenna array formed by two identical isotropic radiators. The total electric field
ET radiated by the two elements assuming no coupling between elements is proportional to
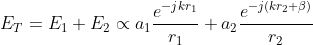 | (Eq. 1) |
where
ai is the magnitude excitation of the
i-th radiator,
β is the difference in phase excitation between the elements,
k is the phase constant (i.e.,
k=2
π/
λ, being
λ the wavelength), and
ri is the distance to the
i-th radiator. Regarding the scheme shown in Fig. 1, and assuming far-field observations, we can do the next approximations
Therefore, Eq. (1) reduces to
%7D%5Cright)) | (Eq. 3) |
 |
| Fig. 1: Geometry of a two-element antenna array (a) and far-field approximation (b). |
With regard to Eq. (3), it can be seen that the total field of the array can be expressed as the field radiated by a single element multiplied by a term that is widely referred as
array factor.
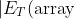%7C=%7CE(%5Cmbox%7Bsingle element%7D)%7C%5Ctimes%7C%5Cmbox%7BArray Factor%7D%7C) | (Eq. 4) |
In the case of our two-antenna system, this array factor (
AF) is obtained as
%7D%5Cright%7C) | (Eq. 5) |
Some practical examples of the
AF of two-antenna arrays are represented in Fig. 2. In the case (a), the
AF of two isotropic elements separated half-wavelength is shown. In such a case, the waves are constructively combined in the directions perpendicular to the array, whereas a null is obtained in the array axis because of waves cancellation. In (b), the case of two elements separated a wavelength is analyzed. In this second case, maximums appear in the array axis and perpendicular to it. The
AF is cancelled at around 30 degrees. The case (c) shows an array with quarter-wavelength separation between elements, and a relative phase delay
β=-
π/4. In this third case, waves are combined in phase in one of the directions of the array axis, and cancelled in the opposite one.
 |
| Fig. 2: Radiation pattern of two omnidirectional elements: (a) separated λ/2, (b) separated λ, and (c) separated λ/4 and β=-π/2. |
N-element linear array
The geometry of a
N-element equispaced linear array is shown in Fig. 3. Let us assume identical amplitudes and that each succeeding element has a progressive phase term
β relative to the preceding one. The array factor in this case can be calculated as
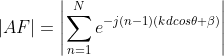 | (Eq. 6) |
The
AF of a
N-element has a maximum when all the signals coming from a given angle
θm combine constructively. It occurs when
kdcos(
θm)+
β=0, that is at
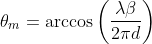 | (Eq. 7) |
Consequently, the radiation pattern of a given array geometry can be pointed to a given direction
θm by modifying the progressive phase difference
β between the elements. The antenna arrays whose direction of maximum radiation can be controlled by adjusting the relative phase term are known as
phased arrays or
scanning arrays.
 |
| Fig. 3: Geometry of an N-element linear antenna array. |
Arrays with arbitrary geometry
References
[1] C. A. Balanis, "Arrays: Linear, Planar, and Circular", in
Antenna Theory: Analysis and Design, 2nd ed. New York, Wiley, 1997.



